Biomedical Science and Research Journals | A Random Walk Model to Evaluate the Post Transcriptional Process in Rett Syndrome

 

A Random Walk Model to Evaluate the Post Transcriptional Process in Rett Syndrome

Abstract

We have proposed a random walk model to model the post-transcription process. We have chosen mature microRNA sequences related to individuals with Rett syndrome. We have analyzed the micro-RNA sequences by transcribing the nucleotides into random fractals. We have reported our results from the exponent, fractal dimension, entropy, and Binder Cumulant. Our analyzes allowed us to report that the system is sensitive to the order of purines and pyrimidines, presenting different measurements from observable physics even for equal purine and pyrimidine proportions

Keywords: Syndrome; RETT Random Paths; Post-Transcription

Introduction

A mental disorder is a syndrome in an individual characterized by clinically significant disorders in cognition, emotional regulation, or behavior that reflect a dysfunction in the psychological, biological, or developmental processes underlying mental functioning. Mental disorders are commonly associated with distress or disability in social, occupational or other important activities.

The diagnosis of a mental illness must be of clinical utility, leading clinicians to determine diagnoses, treatment plans and potential new treatments. There are specific criteria that must be met to diagnose mental disorders such as the following: background validators (similar genetic markers, family traits, temperament, and environmental exposure), competing validators (similar neural substrates, biomarkers, emotional and cognitive processing) and predictive validators (same clinical course - clinical history - and same response to treatment).

Neurodevelopmental disorders are a group of conditions that begin in the developmental period. These developmental disorders typically manifest themselves before the child enters school, characterized by manifestations of personal, social or other occupational activity disabilities. The spectrum of developmental disabilities ranges from specific learning limitations to deficiencies in social skills or intelligence [1, 2, 3, 4, 5, 6].

In particular, Rett syndrome is a neurodevelopmental disorder of genetic etiology, resulting from mutations in the MECP2 (methyl- CpG-binding protein 2) gene found on the X chromosome. Observation of this disease is unrelated to a specific ethnic group. It is prevalent in females, presenting one case every 10,000-20,000. The molecular rationale is that mutated MECP2 encodes a defective protein, incapacitating it to properly perform its biological function.

Thus, genes that should be inactive during specific phases of neuron development remain active, culminating in damage to the central nervous system [7, 8, 9, 10, 11, 12, 13, 14]. The aim of our work is to construct in analogy to the protein coding process. We chose a set of Rett syndrome- related mRNAs. We have used these RNA sequences to construct fractals using discrete random walks as a tool.

Materials and Methods

Inspired by the memory class random walk model, we have proposed a random walk model to construct the random fractal in analogy with the protein coding process [15, 16, 17, 18]. In this model the length of the sequences comprises the total time of the fractal construction. At each instant of time a nucellotide is read and a step is performed by the random walker. Each step performed at the instant of time depends on the entire history of the walker, i.e. it depends on the entire coded RNA sequence. Each state is retrieved equally. The probability of retrieving a past decision at the instant of time is. RNA is called ribonucleic acid. It is a linear polymeric molecule, made up of smaller units called nucleotides, nucleotides receive a dichotomous classification into purines (A and G) and pyrimidines (C and U).

Random tours have well-defined stochastic rules. It occurs as follows: the walker walks one step to the right or one step to the left, with the stochastic evolution equation given by

for the instant of time. When deciding to take a step to the right, that is, the variable σ(t+1) assumes value by stepping left, assume value -1.

The memory is formed of a set of random variables. σ_t ` for the time t’

(a) in the time: t+1, the time: t’ is randomly chosen with uniform probability 1⁄t of the set 1,2, 3,...,t.

(b) σ_(t+1) is determined stochastically by, σ_(t+1) =σ_t ` when reading a pyrimidine e σ_(t+1) =-σ_t ` when reading a purine.

In the time: t=0, the walker is in positionX_0, moves to the right when reading a purine or to the left when reading a pyrimidine, assuming the value, σ1=+1 and σ1=-1,

respectively. In the instant of time: t, the walker moves to the right when reading a purine or to the left when reading a pyrimidine, assuming the value: σt’=+1 e σt’=-1, respectively. Walker position is quantified by the stochastic evolution equation:

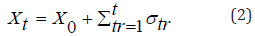
We have performed numerical experiments using them to obtain measurements of the following observable physics such as skewness, kurtosis, Hurst exponent, fractal dimension, information entropy, and fourth order Binder cumulative.

Skewness measures how much a distribution is deviated to the right or left from the distribution mean. It is measured by following the formula:

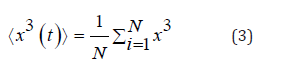
Kurtosis is a measure of whether the data are heavy-tailed or light-tailed relative to a normal distribution. Kurtosis is quantified according to the following stochastic equation:

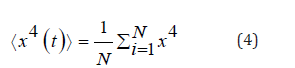
The Hurst’s exponent serves to classify Anomalous diffusion can be classified as superdiffusive (H>1⁄2), normal diffusive(H=1⁄2) and subdifusive(H<1⁄2)

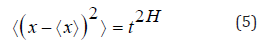
The fractal dimension (D) is a measure of roughness while(H) is a quantity that classifies the diffusion regimes. The fractal dimension is related to the Hurst exponent by the following equation:

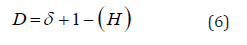
in which δ is the dimension in Euclidean space in this case (δ=1). The information entropy measures the overall effect of bit variation associated with random walks. Information entropy is described by the equation:

in which Wk (x,t) is the probability distribution of finding random walkers in the position x and in the time: t [19].

Binder cumulant is a quantity widely used in the analysis of phase transition systems [20]. In our system we have analyzed the fourth order Binder cumulant in the context of the protein coding analogy according to the Rett syndrome RNA sequences employed to construct random fractals. Binder cumulant is quantified according to the formula:

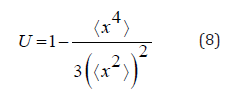
We have measured these observable physics based on the RNA sequence data in the (Table 1).

Results

We have performed measurements of skewness, flatness, Hurst exponent, fractal dimension, entropy of information and fourth order Binder cumulant. In the (Figure 1), (Figure 2), (Figure 3), (Figure 4) we have presented the measurements of skewness, Hurst exponent, fractal dimension and entropy of information as a function of the label assigned to each RNA sequence presented in the (Table 1).

In the (Figure 1), we have presented typical mediated skewness. We have noted that for the 23 sequences analyzed, 15 show positive symmetry of the probability distribution, i.e., pyrimidines have a macroscopically outstanding effect over purines. While 8 sequences have negative skewness, therefore, in these cases purines have a macroscopically outstanding effect over pyrimidines.

(Figure 2)& (Figure 3)show typical measurements of the Hurst exponent and fractal dimension. These quantities are inverse functions of each other as it was shown in the equation. (6). We have noted that there is no relationship between the skewness measurements shown in the (Figure 1). Besides, we have noted that random walks have a predominantly subdifusive regime characterized by typical measurements of, which are accompanied by roughness measurements in the range of (1.5Figure 3).

In the (Figure 4), we have presented typical measures of information entropy. Entropy measurements are related to the Hurst exponent and the fractal dimension of the system. We have noted that the larger (smaller) the measurements observed for the Hurst exponent (the fractal dimension), the smaller the entropy variations. The largest entropy variation occurred for the sequence with ID hsa-miR-296-3p, being equal abits, which has a percentage of 39.13% purines and 60.87% pyrimidines.

For information entropy, we have observed three typical behaviors in the construction of random walks, which are presented In the (Figure 5). In general, entropy from zero variation, ie at the beginning of nucleotide reading and grows to a point where it remains with a fixed range of bits. Entropy variations occur in three typical ways presented In the (Figure 5), (Figure 5), (Figure 5c) showing the results of entropy variation reading the RNA sequences with ID dre- -mir-146a, hsa-miR-122-3p and hsa-miR-296-3p, respectively. For the dre-mir-146a, hsa-miR-122-3p and hsa-miR-296-3p sequences the entropy exhibits sigmoid behavior with saturation points equal to and bits, accompanied by larger fractal dimension values equal to, and respectively. The dre-mir-146a sequence shows smoother growth for entropy, while the hsa-miR-122-3p sequence has more abrupt growth, as can be seen from the curve In the (Figure 5b). The entropy of the hsa-miR-296-3p sequence grows faster than the sequences of (Figure 5), (Figure 5), We have also noticed that even though curve (Figure 5) has a higher saturation point, curve (Figure 5) grows faster but stabilizes first. This fact can be explained by looking at the results In the figure 6. In the (Figure 6), the ordinary Binder cumulative measurements are presented. The term responsible for such variations is the (⟨x2⟩)2 , because according to our observations the kurtosis is invariant for all the averages that we have made, and it is equal to ⟨x4⟩=214.748. Note that, for curve (Figure 6), the Binder cumulant grows to saturation point, while curves (Figure 6), (Figure 6) have points the cumulant has a lower concave region. , then grows reaching the saturation points each. Besides, we have noticed that the bigger this region is concave, the greater the initial entropy variation, as can be seen in curves (Figure 5a & 5c), (Figure 6), (Figure 6).

Discussion

We have studied Rett syndrome from a stochastic perspective, performing a process of constructing fractal objects through an analogy between protein coding and random class walks with memory. This method was used to be used as a tool for analysis and diagnosis of Rett syndrome, observing some RNA sequences related to the post-transcription process responsible for protein coding. We observed that typical skewness measurements are not related in this problem as averages of Hurst exponent and fractal dimension.

Kurtosis remains invariant for all the measurements we have made. Therefore, skewness and flatness measurements are shown without any impact to extract pertinent information to analyze Rett syndrome. Furthermore, we have observed that lower Hurst exponent values are accompanied by higher fractal dimension averages (higher roughness) and greater entropy variations. Random walks present the classification of their regime as subdifusive, constructing a fractal object with the dimension between a straight line and a plane. Surprisingly, it is noted that the entropy measurements are related to the Binder cumulative measurements. The emergence of a concave region in the cumulant is related to greater variations in entropy, and the larger the concave region, the greater the variations in entropy.

Acknowledgment

We would like to thank FAPESPA for supporting our research.

For More information: https://biomedgrid.com/fulltext/volume6/a-random-walk-model-to-evaluate-the-post-transcriptional-process-in-rett-syndrome.001092.php

Know More Information: Biomed Grid Please Click on : https://biomedgrid.com

For More information: Open Access Journals of Biomedical Science and Research: Journal of Biomedical Science 

Know More Information: Biomed Grid Please Click on : https://biomedgrid.com